EzoBox.ruБиблиотека эзотерики

Итак, с кругом все просто: центральный кол и ременная (веревочная) петля, длина которой равна диаметру круга. Все просто рассчитать и просто — оставляя в стороне техническо-бытовые проблемы — реализовать.

С эллипсом все значительно сложнее. В рамках аналитической геометрии форма эллипса элементарно описывается в параметрическом виде, чуть сложнее — в полярных координатах, очень сложно — привычных декартовых. Но древние строители мегалитов, как мы уже упоминали, вряд ли владели высшей математикой; зато в их распоряжении были вторичные свойства кривых: так, например, описанный выше очевидный способ построения окружности основан на том, что окружность — это геометрическое место точек, равноудаленных от некоей точки, которая и является ее центром.

В отличие от окружности, эллипс определяется не одной точкой-центром, но двумя точками, которые называются его фокусами и лежат на главной (длинной) его оси. Уникальное свойство эллипса заключается в том, что сумма расстояний от любой его точки до фокуса-1 и до фокуса-2 неизменна. А поскольку расстояние между фокусами неизменно по определению, то это дает нам (и нашим предкам) способ построения эллипса на местности, минуя хитрости аналитической геометрии. Достаточно вбить в землю два столба, накинуть на них все ту же ременную петлю и обойти, удерживая петлю в натяжении, эти столбы вокруг: фигура, которую очертит на земле ввязанный в петлю колышек, и будет эллипсом!

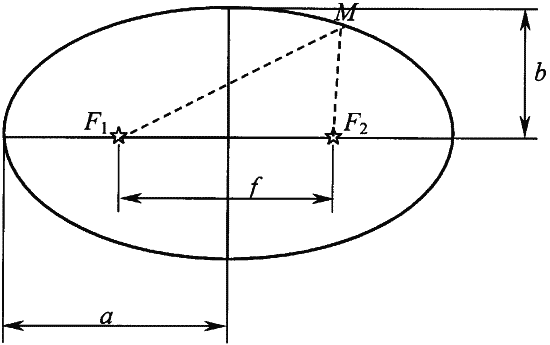
Просто? Отнюдь нет. Проблема заключается в том, что требуется-то не произвольный эллипс, а эллипс с более или менее заданными длиной и шириной (вряд ли каменные круги, на сооружение которых нередко уходили десятилетия, а то и века, создавались «просто так», наобум). Геометрическая задача: на каком расстоянии нужно расположить столбы-фокусы, чтобы получить, следуя вышеописанной технологии, эллипс с нужными длиной и шириной?

Сейчас эта задачка решается элементарно: несложно показать, что длина эллипса, его ширина и расстояние между фокусами связаны теоремой Пифагора, т. е.:

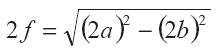
Определив таким образом расстояние между столбами, несложно посчитать и требуемую длину петли — она будет равна расстоянию между столбами плюс заданную длину каменного эллипса (говоря современным языком — удвоенной сумме фокального расстояния и большой полуоси эллипса).

Но все это легко в XXI веке, когда теорему Пифагора изучают едва не в начальных классах школы. Строители же мегалитов вряд ли владели теоремой Пифагора, какой бы простой она ни казалась нам. Что же оставалось им — очевидно, древнейший и многократно проверенный практикой путь эмпирики, путь «проб и ошибок». Иначе говоря, им требовалось опытным путем подобрать такое соотношение между длинами трех отрезков, чтобы, сложенные концами, они образовывали прямоугольный треугольник, — тогда его гипотенуза будет пропорциональна длине эллипса, один из катетов — ширине эллипса, а другой — искомому расстоянию между столбами. И уж конечно, таковое соотношение должно выражаться целыми числами — вряд ли тысячи лет назад строителям мегалитов было удобно работать с дробями…