EzoBox.ruБиблиотека эзотерики

Наконец это случилось! До сих пор круги на полях и научные круги никак не пересекались. А теперь пересеклись! По крайней мере, о кругах на полях заговорили в научном журнале. И не просто и научном журнале, но именно в МАТЕМАТИЧЕСКОМ разделе!

Похоже, эти круги передают нам теоремы, которых не оставил сам Евклид. На следующей странице приведена статья из научного журнала «Сайнс ньюз».

Несколько лет назад астроном Джеральд С. Хокинс из Бостонского университета обратил внимание на то, что некоторые узоры кругов на полях представляют собой зашифрованные теоремы, описывающие числовые взаимоотношения между различными параметрами кругов, треугольников и других фигур, из которых состоят узоры.

Хокинс обнаружил, что, опираясь на изображения определенных узоров и используя принципы Евклидовой геометрии, он может доказать четыре теоремы. Затем^[40]он открыл пятую, более общую теорему, из которой следуют предыдущие четыре.

Как ни странно, Хокинс не обнаружил описание этой теоремы ни в трудах Евклида, ни в других книгах по геометрии, к которым он обращался. Когда он предложил читателям научных журналов«Сайнс ньюз»и«Мэтимэтикс тичер»вывести эту нигде не опубликованную теорему, опираясь на другие четыре теоремы, являющиеся ее следствием, решения не предложил никто.

Однако прошлым летом создатели кругов на полях «продемонстрировали свое знакомство с этой пятой теоремой», — сообщает Хокинс. Среди десятков узоров, образовавшихся на полях Англии, по меньшей мере один изображает теорему Хокинса.

Люди, столь причудливым образом реализующие свои математические таланты, пока еще не известны. Их работа демонстрирует недюжинное знание Евклидовой геометрии, изумительную способность тайно пробираться на поля; сгибать стебли растений, не поломав их; выполнять сложные необычайно точные чертежи с использованием палки и веревки — причем под покровом темноты^[41]!

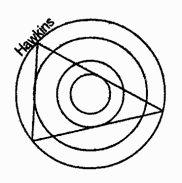
Графическое изображение теоремы Хокинса представляет собой несколько концентрических кругов — в один из них вписан треугольник, чьи стороны являются касательными по отношению к трем другим кругам… Точно такое же изображение наблюдалось на одном из кругов на полях. На трех равнобедренных треугольниках основываются и некоторые другие геометрические узоры на полях.

Обратите внимание на последний абзац этой математической статьи. Ого! Оказывается, два парня с досками и веревками не просто вытаптывают десятки кругов среди посевов (иногда составляя композиции в два футбольных поля длиной), но к тому же являются прекрасными математиками и зашифровывают в своих произведениях новые теоремы — неизвестные даже Евклиду!

Как во Второй, так и в Третьей Книгах Крайона я сообщал о необъяснимом гамма-излучении и цитировал научные источники. Почему? В главе восьмой Книги Второй (1994) Крайон говорил, что именно это явление будет свидетельствомпоступления духовной энергии на планету:«Ищите кратковременное необъяснимое гамма-излучение высокой интенсивности».